指数 分数 微分 315371-指数 ���数 微分
2
他の三角関数についての難しい微分計算は >sin,cos,tanの微分例題を解説!2乗、分数のときにはどうやる? こちらの記事でまとめているのでご参考ください。 指数、対数関数の導関数 指数函数积分MIT—微分方程笔记06 复数及复指数 三少爷的键 工科顶级学渣 9 人 赞同了该文章 第06讲 复数及复指数 Complex Numbers and Complex Exponentials 本讲介绍复数和复指数,复数 ,其 共轭复数 为 ,两者乘积为 ,在复数的 除法 中经常要用到这个运算。 例: 极坐标形式
指数 分数 微分
指数 分数 微分- 指数函数的积分公式是 ∫e^x dx = e^xc ∫e^(x) dx = e^xc (c为常数) 因为e^x的微分还是e^x,所以上面的积分可以直接得到~ 在这里补充一下一般指数函数的积分: y=a^x 的积分为 (a^x)/ln(a) c扩展资料 积分是微分的逆运算,即知道了函数的导函数,反求原函数。対数微分法 例題1 \y = \sqrt{(x 1)(x 2)}\tag{♪}\ (♪) の関数を例に対数微分法を説明していきます。(♪) は直接微分してもそれほど難しい計算になりませんが,まずは扱いやすい関数を例に対数微分法を理解しましょう。

分数微分公式
2 分数の微分の解説 まずは分数の微分公式から見ていきたいと思います。 この公式について理解するコツは、分母が関数の分数を、以下の通り、1 を指数とする べき乗 ・・・ に置き換えることにあり 指数関数の微分 任意の a > 0 a > 0 a > 0 に対して y = a x y=a^x y = a x の導関数は, y ′ = a x log a y'=a^x\log a y ′ = a x lo g a である。 この公式を4通りの方法で証明します! 対数関数の微分 基本対数関数の微分 で見たように、対数関数の微分で一番重要なものは、 (logx)′ = 1 x ( log x) ′ = 1 x です。 底が e e でない場合は、底の変換を行ってから計算するようにします。 これを踏まえて、次の問題を考えましょう
微分とは? 微分とは、 ある関数 \(f(x)\) の導関数 \(f'(x)\) を求める演算 のことです。 さて、では導関数って何?と思いますよね。 導関数とは、関数 \(y = f(x)\) のある点における瞬間の変化率(すなわち接線の傾き)を求められる関数で、次のように定義されます。第一讲 分数阶微分方程 主要参考资料4,5,7 11 分数阶导数 分数阶导数(Fractionalderivatives)有多种定义方式,常用的有RiemannLiouville分数阶导数,Caputo分 数阶导数,GrünwaldLetnikov分数阶导数,等等 下面我们就对以上三种定义进行分别介绍,更多定义可参 见3マイナス乗の微分 例3:f(x) = 1 x2 f(x) = 1 x2 = x−2 ···指数表記 ∴ f′(x) = ¡ x−2 ¢′ = −2x−3 ···微分公式 = − 2 x3 ···分数表記(できればここまで:中学生でも意味がわかるので) 問2 上の例にならって、次の関数を微分しなさい。 1 f(x) = 1 x4 = ←ここに指数表記をつづけて書く(小問2
指数 分数 微分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
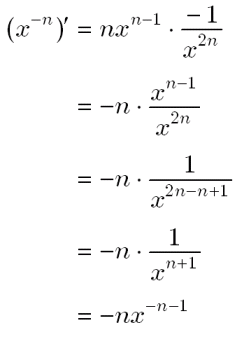 |  | |
 |  | |
 |  |  |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
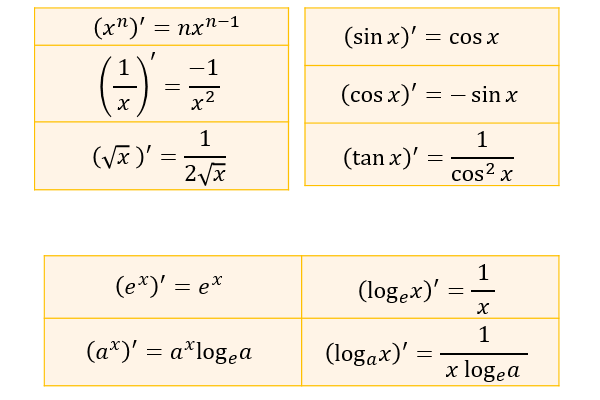 | ||
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
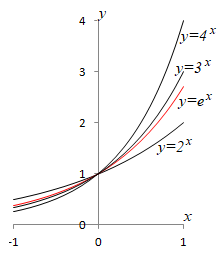 |  | |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「指数 分数 微分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
具体例で学ぶ数学 > 微積分 > 微分の公式全59個を重要度つきで整理 最終更新日 このページでは、微分に関する公式を全て整理しました。 基本的な公式から、難しい公式まで59個記載しています。 重要度★★★ :必ず覚える 重要度★★☆ :すぐ指数関数の微分 1.対数微分法を用いる 2.eに底を変換して微分する 指数関数を微分する場合,底を自然対数の底 e に変換してから,微分するとよい. 例 底が a である a x を,底を e に変換して微分する. (ただし, a は0より大きい定数)
Incoming Term: 指数 分数 微分,
No comments: